電気回路とは
電気回路とは、電気を流す通路である。
この回路は電子部品と呼ばれるもので構成され、電気の流れを制御している。
イメージしやすいように、電気の流れを水の流れで例えられる。
例えば、浄水場から水道まで水圧により水が送り込まれている。
私たちは蛇口を捻る、つまり抵抗を変化させることによって水量を調整し水を汲みだしている。
同様に電気の場合でも、電圧が一定であれば、電流が抵抗によって変化する。
この電圧と電流、抵抗の関係を‘”オームの法則”というもので表すことができる。
オームの法則
オームの法則は以下の式で定義される。
V = R・I
V:電圧(単位はボルト[V]。一定の抵抗に対してどれだけの電流が流せるかという能力)
I:電流(単位はアンペア[A]。電気の流れ。値が大きいほどたくさん電気が流れている)
R:抵抗(単位はオーム[Ω]。電気の流れを妨げるもの)
この式を乾電池につなげた豆電球で考えてみる。
下図のRが豆電球の抵抗、Vが乾電池の起電力(電圧)、Iが乾電池によって流れた電気(電流)を表している。
このような図を回路図と呼ぶ。
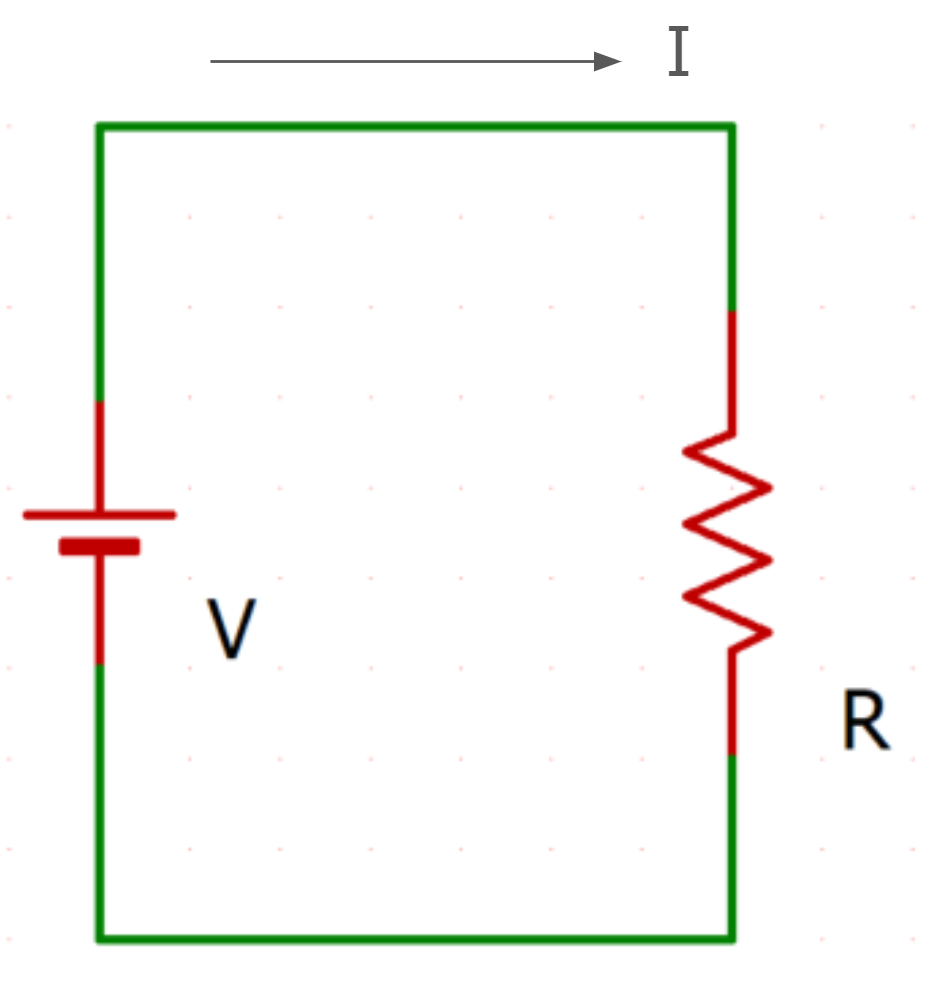
オームの法則を使えば、電圧と抵抗が分かれば電流を求めることができる。
例として乾電池は1.5V、豆電球の抵抗は3Ω一定とすると、
オームの法則により、電流値は
V = R・I
I = R / I
= 3/1.5 =2 [A]
となる。
また、この抵抗Rには電流Iが流れているため、Rの両端にはR・I=1.5Vの電圧(乾電池の電圧と同じ値)が電流の方向と逆方向にかかっている。
これを逆起電力と呼び、加えられた電圧Vと平衡する関係を持つ。
つまり、乾電池によって印加された電圧1.5Vは豆電球の抵抗Rで1.5V下がり、乾電池のマイナス端子(回路の終端)では0Vになる。
逆起電力という考え方は、力学でいう反作用に対応するもので今後常に利用するものである。
このオームの法則と逆起電力の考え方から、抵抗が複数繋がっている場合でも解くことができる。
抵抗のつなぎ方は、直列接続と並列接続と呼ばれる基本的なものとして2つある。
直列接続
直列接続とはその名の通り、複数の部品を1つの電流の通り道に接続したものである。
下図のように抵抗を2つ直列に繋いだ場合を考える。
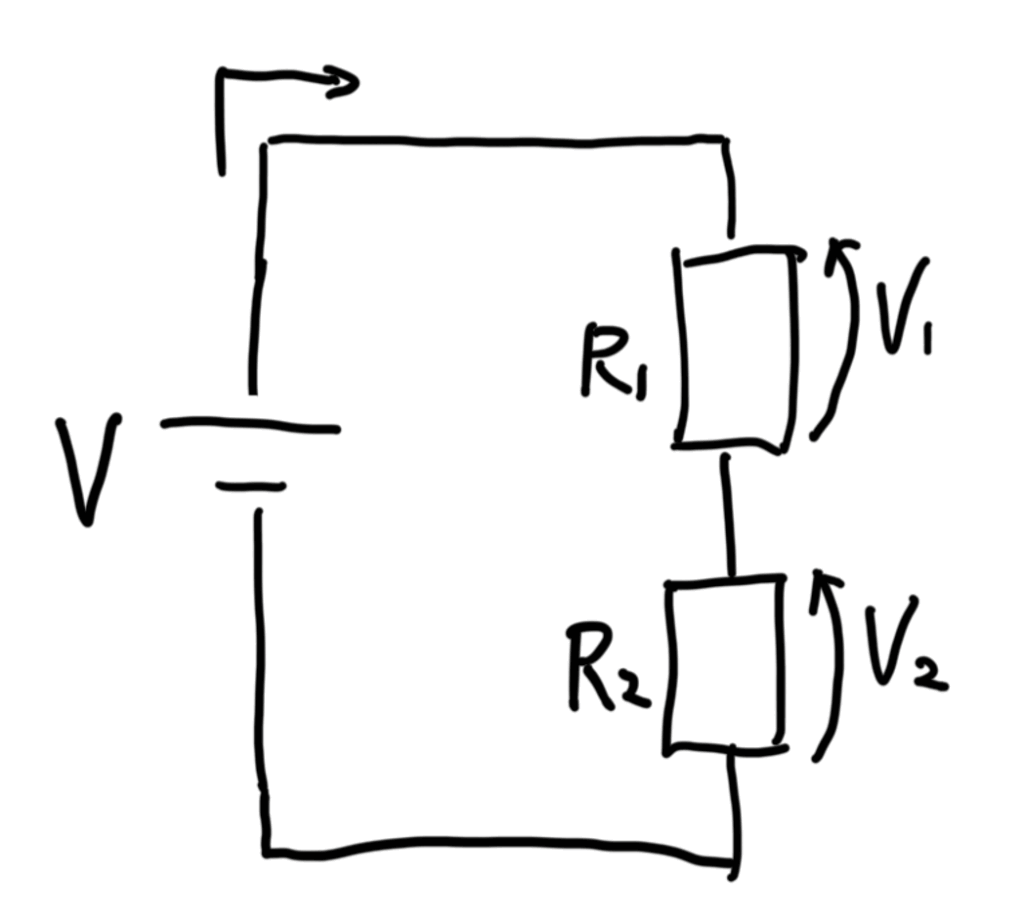
オームの法則より、次の関係が成立する。
V = V1 + V2
V1 = I ・ R1
V2 = I ・ R2
上記方程式から、
V =(R1+R2)I
全体の抵抗(合成抵抗)Rとして考えれば
V = R・I =(R1+R2)I
となる。
よって、複数の抵抗が直列接続されているとき
全体の抵抗(R)=各抵抗(R1+R2+R3+…)
が成り立つ。
並列接続
並列接続とはその名の通り、複数の部品を横に並べて接続したものである。
下図のように抵抗を2つ並列に繋いだ場合を考える。
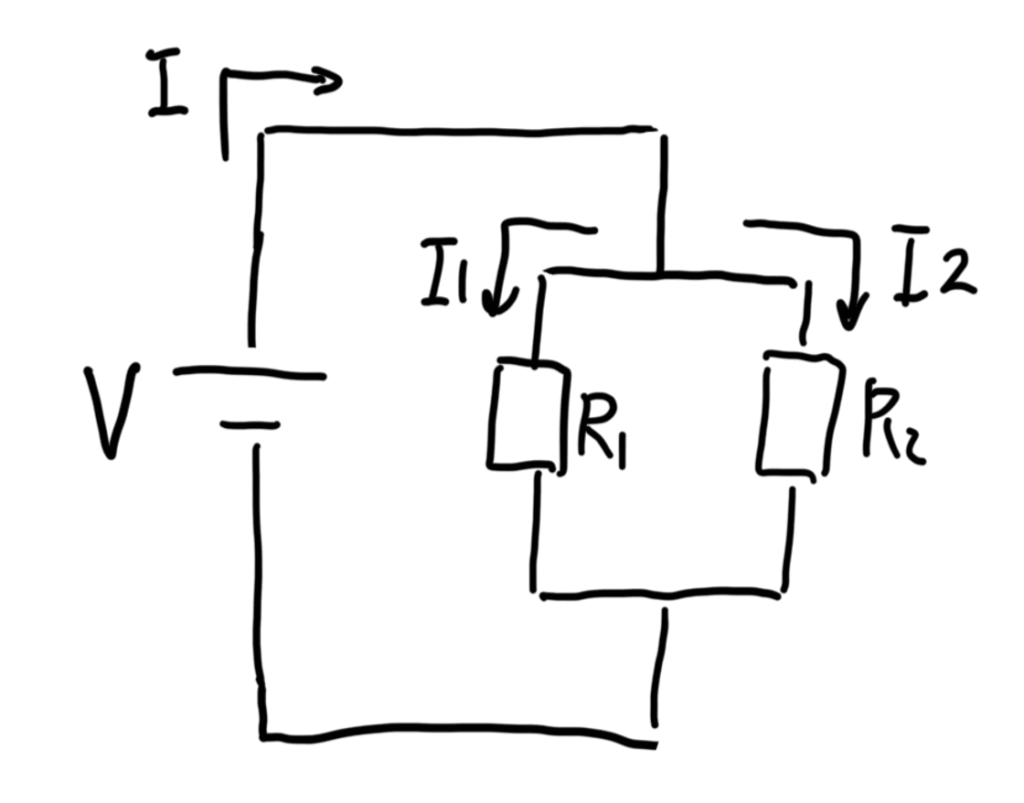
オームの法則より、次の関係が成立する
V = I1・R1
V = I2・R2
また、全体の電流をI、全体の抵抗Rとすれば
I = I1+I2=V/R
上記より、
V/R1 + V/R2 = V/Rから
全体の抵抗(合成抵抗)Rとして考え
1/R = 1/R1 + 1/R2
よって、複数の抵抗が並列接続されているとき
1/R = 1/R1 + 1/R2 + 1/R3 +…
が成り立つ。



コメント